Reviving a failed network through microscopic interventions

From mass extinction to cell death, complex networked systems often exhibit abrupt dynamic transitions between desirable and undesirable states.
These transitions are often caused by topological perturbations (such as node or link removal, or decreasing link strengths). The problem is that reversing the topological damage, namely, retrieving lost nodes or links or reinforcing weakened interactions, does not guarantee spontaneous recovery to the desired functional state. Indeed, many of the relevant systems exhibit a hysteresis phenomenon, remaining in the dysfunctional state, despite reconstructing their damaged topology. To address this challenge, we develop a two-step recovery scheme: first, topological reconstruction to the point where the system can be revived,
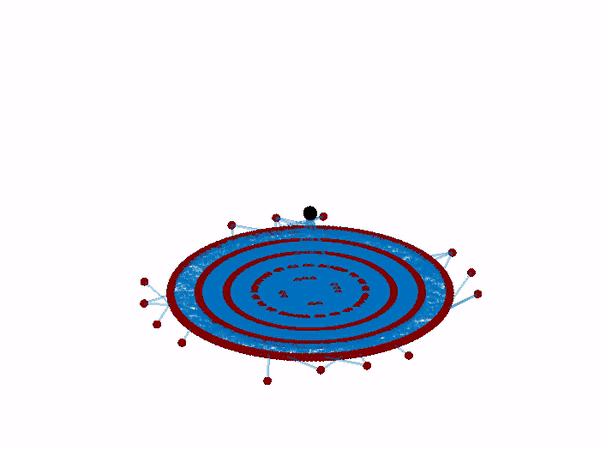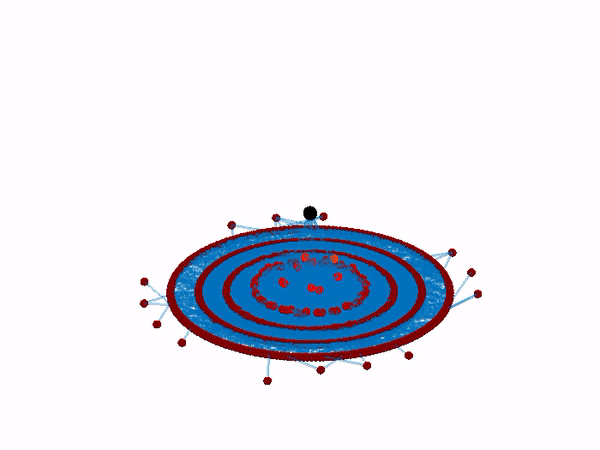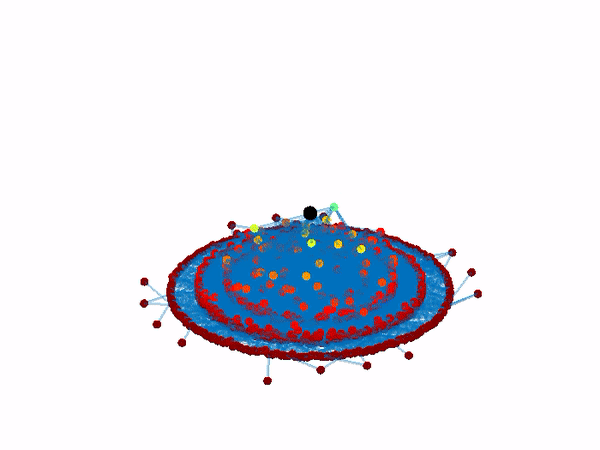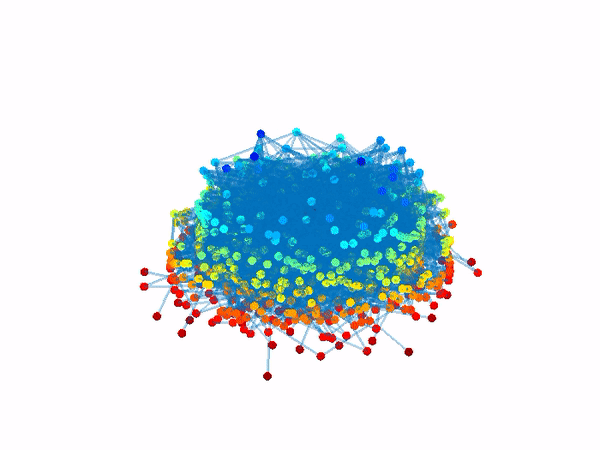
and then dynamic interventions to reignite the system’s lost functionality by controlling the activity of just a single node or a few nodes.
By applying this method to a range of nonlinear network dynamics, we identify the recoverable phase of a complex system, a state in which the system can be reignited by microscopic interventions, for instance, controlling just a single node. Mapping the boundaries of this dynamical phase, we obtain guidelines for our two-step recovery.
Epidemics on evolving networks with varying degrees
Epidemics on complex networks is a widely investigated topic in the last few years, mainly due to the last pandemic events. Usually, real contact networks are dynamic, hence much effort has been invested in studying epidemics on evolving networks. We propose and study a model for evolving networks based on varying degrees, where at each time step a node might get, with probability r, a new degree and new neighbors according to a given degree distribution, instead of its former neighbors.
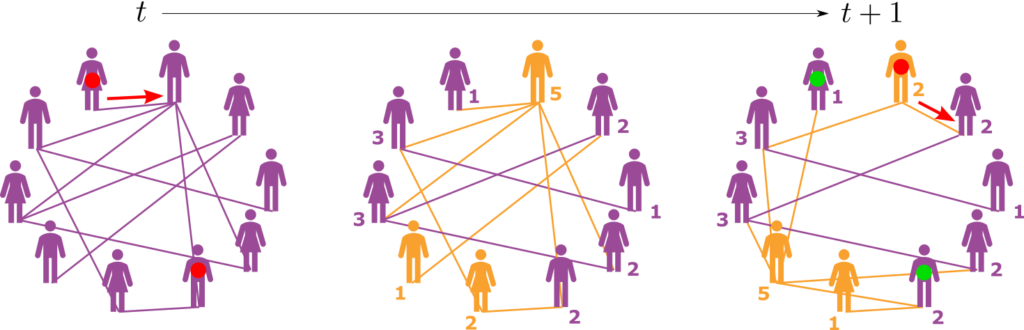
We find analytically, using the generating functions framework, the epidemic threshold and the probability for a macroscopic spread of disease depending on the rewiring rate r. Our analytical results are supported by numerical simulations. We find surprisingly that the impact of the rewiring rate r has qualitative different trends for networks having different degree distributions. That is, in some structures, such as random regular networks the dynamics enhances the epidemic spreading while in others such as scale-free the dynamics reduces the spreading. In addition, for scale-free networks, we reveal that fast dynamics of the network, r = 1, changes the epidemic threshold to nonzero rather than zero found for r < 1, which is similar to the known case of r = 0, i.e., a static network. Finally, we find the epidemic threshold also for a general distribution of the recovery time.
